Линейная магнитная сборка Халбаха, состоящая из пяти сегментов

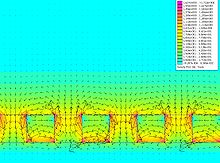
Магнитная сборка Хальбаха — особая конфигурация постоянных магнитов, характеризующаяся тем, что магнитное поле с одной стороны практически полностью отсутствует благодаря особому расположению элементов сборки.^[1]

Повторение последовательности элементов (на передней поверхности вектор намагничивания: влево, вверх, вправо, вниз, влево) воспроизводит описываемый эффект.

Эффект был открыт Маллинсоном в 1973 году и был названы им удивительным, что, тем не менее, не помешало ему распознать в нём способ потенциального улучшения свойств и качеств записи на магнитную ленту.^[2]

В 1980-х годах Клаус Хальбах, в то время физик Национальной лаборатории им. Лоуренса разработал магнитную сборку, впоследствии названную его именем и предназначенную для мощного излучения пучком элементарных частиц в ускорителе.^[3]

Одномерные сборки Хальбаха[править | править вики-текст]

Намагничивание[править | править вики-текст]

Распределение магнитного поля может быть представлено при помощи чертежей Маллинсона. Чертежи показывают магнитное поле, вызванное полоской поверхностью ферромагнитного материала с переменным вектором намагничивания по координате y (верхний левый чертёж) и по координате x (верхний правый чертёж). Обратите внимание на то, что поле в верхней полуплоскости обоих чертежей имеет одинаковую направленность, в то время как в нижней полуплоскости — противоположную. В результате суперпозиции магнитных полей двух структур получается структура, магнитное поле которой изображённо на нижнем чертеже:

Поле вокруг отдельных элементов сборки

Основной смысл сборки заключается в том, что компенсация магнитного потока снизу сборки приводит к его усилению сверху. В принципе, любая сборка, в которой компоненты магнетизированы с поворотом фазы ${\displaystyle \pi /2}$ приводит к усилению магнитного потока с одной стороны сборки. Математические преобразования, в которых сдвиг фазы всех компонентов относительно друг друга составляет ${\displaystyle \pi /2}$ называется преобразованием Гильберта. Таким образом, вектор намагниченности компонентов должен составлять пары в преобразовании Гильберта (простейший случай — функции ${\displaystyle \sin(x)\cos(y)}$, как это показано на рисунке выше).

Можно выделить два основных преимущества в одностороннем магнитном потоке:

• Наверху сборки магнитный поток в два раза интенсивнее (в идеальном случае);
• Внизу магнитной сборки магнитный поток отсутствует (опять же в идеальном случае, при условии сборки бесконечной длины), а это серьёзно упрощает разработку систем.

Магнитная сборка Халбаха может быть легко «развёрнута» в цилиндр Халбаха.

Поле сверху бесконечно длинной сборки может быть записано функцией вида:^[4]

${\displaystyle F(x,y)=F_{0}e^{i\lambda x}e^{-\lambda y}}$,

где

${\displaystyle F(x,y)}$ — функция поля, вида ${\displaystyle F_{x}+F_{y}i}$

${\displaystyle F_{0}}$ — амплитуда поля на поверхности сборки

${\displaystyle \lambda }$ — пространственная частота

Цилиндр Хальбаха[править | править вики-текст]

Сфера Хальбаха[править | править вики-текст]

Примечания[править | править вики-текст]

Ссылки[править | править вики-текст]

• [1]

Литература[править | править вики-текст]

• Z. Q. Zhu, D. Howe «Halbach permanent magnet machines and applications: a review», 2001, ISSN 1350-2352

См. также[править | править вики-текст]

• Магнит
• Магнитное поле

Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её.